
Умножение на матрицу
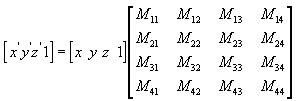
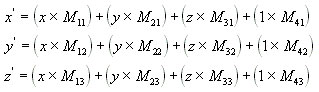
Типы матриц
Не следует понимать заголовок этой части текста так, будто есть совершенно разные и особенные типы матриц, которые чем-то совершенно уникальны. Я называю их типами просто для удобства – на самом деле матрица, она и есть матрица и отличаются матрицы лишь значениями их отдельных элементов, не более того. При этом так же надо что бы Вы понимали, что я стараюсь объяснять “на пальцах”, так, что бы понял каждый – с математической точки зрения всё, мягко говоря, несколько сложнее. Я же лишь просто расскажу и покажу то, что Вам нужно знать для того, что бы Вы могли не испытывать особых трудностей с матричной арифметикой и могли понимать как работают преобразования вертексов/моделей/нормалей и т. д. в ваших программах.
Итак, матрицы можно разделить на четыре условных типа:
Матрицы сдвига Матрицы вращения Матрицы масштабирования Прочие матрицы (например, перспективные или комбинированные из первых трёх типов)
Матрицы сдвига (Translate Matrix)
Матрицы сдвига это самое простое, что только можно себе представить. Они задают просто “сдвиг” по каждой из осей координат на определённое значение. Этот сдвиг хранится в нижней строке матрицы (в первых трёх её значениях, которые выше обозначены как М41, М42, М43). Если мы зададим в них, например (0, 10, 99), то в результате трансформации любого вектора этой матрицей, он сдвинется на 0 по оси X, на 10 по оси Y и на 99 по оси Z. Мне кажется, совсем не сложно, правда же?
Матрицы масштабирования (Scale Matrix)
Что делают матрицы этого типа, тоже совсем несложно догадаться – они масштабируют. Коэффициенты масштабирования вдоль каждой оси задаются диагональными элементами матриц: М11 для оси X, М22 для оси Y и М33 для оси Z.
Матрицы вращения (Rotate Matrix)
Этот тип матриц несколько сложнее, чем предыдущие. Потому и понять его надо получше, разобраться что к чему и из чего оно следует. Для вращения 2х-мерного вектора, как известно, используется такая формула:
